Энтропия
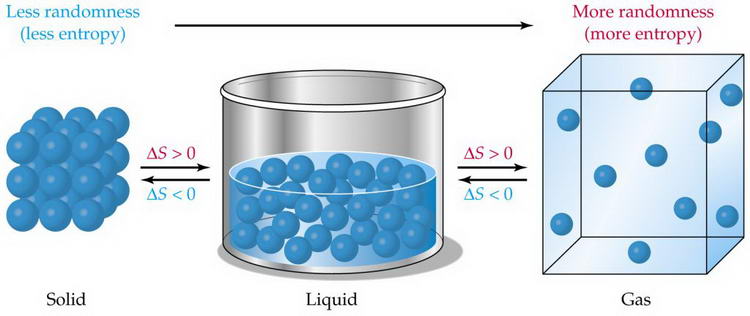
Энтропия (от др.-греч. ἐντροπία «поворот», «превращение») – широко используемый в естественных и точных науках термин. Впервые введён в рамках термодинамики как функция состояния термодинамической системы, определяющая меру необратимого рассеивания энергии. В статистической физике энтропия характеризует вероятность осуществления какого-либо макроскопического состояния. Кроме физики, термин широко употребляется в математике: теории информации и математической статистике.
В науку это понятие вошло ещё в XIX веке. Изначально оно было применимо к теории тепловых машин, но достаточно быстро появилось и в остальных областях физики, особенно, в теории излучения. Очень скоро энтропия стала применяться в космологии, биологии, в теории информации. Различные области знаний выделяют разные виды меры хаоса:
- информационная;
- термодинамическая;
- дифференциальная;
- культурная и др.
Например, для молекулярных систем существует энтропия Больцмана, определяющая меру их хаотичности и однородности. Больцман сумел установить взаимосвязь между мерой хаоса и вероятностью состояния. Для термодинамики данное понятие считается мерой необратимого рассеяния энергии. Это функция состояния термодинамической системы. В обособленной системе энтропия растёт до максимальных значений, и они в итоге становятся состоянием равновесия. Энтропия информационная подразумевает некоторую меру неопределённости или непредсказуемости.
Энтропия может интерпретироваться как мера неопределённости (неупорядоченности) некоторой системы, например, какого-либо опыта (испытания), который может иметь разные исходы, а значит, и количество информации. Таким образом, другой интерпретацией энтропии является информационная ёмкость системы. С данной интерпретацией связан тот факт, что создатель понятия энтропии в теории информации (Клод Шеннон) сначала хотел назвать эту величину информацией.
Для обратимых (равновесных) процессов выполняется следующее математическое равенство (следствие так называемого равенства Клаузиуса), где – подведенная теплота, – температура, и – состояния, и – энтропия, соответствующая этим состояниям (здесь рассматривается процесс перехода из состояния в состояние ).
Для необратимых процессов выполняется неравенство, вытекающее из так называемого неравенства Клаузиуса, где – подведенная теплота, – температура, и – состояния, и – энтропия, соответствующая этим состояниям.
Поэтому энтропия адиабатически изолированной (нет подвода или отвода тепла) системы при необратимых процессах может только возрастать.
Используя понятие энтропии Клаузиус (1876) дал наиболее общую формулировку 2-го начала термодинамики: при реальных (необратимых) адиабатических процессах энтропия возрастает, достигая максимального значения в состоянии равновесия (2-ое начало термодинамики не является абсолютным, оно нарушается при флуктуациях).

Абсолютная энтропия (S) вещества или процесса – это изменение доступной энергии при теплопередаче при данной температуре (Btu/R, Дж/К). Математически энтропия равняется теплопередаче, деленной на абсолютную температуру, при которой происходит процесс. Следовательно, процессы передачи большого количества теплоты больше увеличивают энтропию. Также изменения энтропии увеличатся при передаче теплоты при низкой температуре. Так как абсолютная энтропия касается пригодности всей энергии вселенной, температуру обычно измеряют в абсолютных единицах (R, К).
Удельную энтропию (S) измеряют относительно единицы массы вещества. Температурные единицы, которые используются при вычислении разниц энтропии состояний, часто приводятся с температурными единицами в градусах по Фаренгейту или Цельсию. Так как различия в градусах между шкалами Фаренгейта и Ренкина или Цельсия и Кельвина равные, решение в таких уравнениях будет правильным независимо от того, выражена энтропия в абсолютных или обычных единицах. У энтропии такая же данная температура, как и данная энтальпия определенного вещества.
Подводим итог: энтропия увеличивается, следовательно, любыми своими действиями мы увеличиваем хаос.

Просто о сложном
Энтропия – мера беспорядка (и характеристика состояния). Визуально, чем более равномерно расположены вещи в некотором пространстве, тем больше энтропия. Если сахар лежит в стакане чая в виде кусочка, энтропия этого состояния мала, если растворился и распределился по всем объёму – велика. Беспорядок можно измерить, например, посчитав сколькими способами можно разложить предметы в заданном пространстве (энтропия тогда пропорциональна логарифму числа раскладок). Если все носки сложены предельно компактно одной стопкой на полке в шкафу, число вариантов раскладки мало и сводится только к числу перестановок носков в стопке. Если носки могут находиться в произвольном месте в комнате, то существует немыслимое число способов разложить их, и эти раскладки не повторяются в течение нашей жизни, как и формы снежинок. Энтропия состояния «носки разбросаны» – огромна.
Второй закон термодинамики гласит, что самопроизвольно в замкнутой системе энтропия не может убывать (обычно она возрастает). Под её влиянием рассеивается дым, растворяется сахар, рассыпаются со временем камни и носки. Эта тенденция объясняется просто: вещи движутся (перемещаются нами или силами природы) обычно под влиянием случайных импульсов, не имеющих общей цели. Если импульсы случайны, всё будет двигаться от порядка к беспорядку, потому что способов достижения беспорядка всегда больше. Представьте себе шахматную доску: король может выйти из угла тремя способами, все возможные для него пути ведут из угла, а прийти обратно в угол с каждой соседней клетки – только одним способом, причём этот ход будет только одним из 5 или из 8 возможных ходов. Если лишить его цели и позволить двигаться случайно, он в конце концов с равной вероятностью сможет оказаться в любом месте шахматной доски, энтропия станет выше.
В газе или жидкости роль такой разупорядочивающей силы играет тепловое движение, в вашей комнате – ваши сиюминутные желания пойти туда, сюда, поваляться, поработать, итд. Каковы эти желания – неважно, главное, что они не связаны с уборкой и не связаны друг с другом. Чтобы снизить энтропию, нужно подвергнуть систему внешнему воздействию и совершить над ней работу. Например, согласно второму закону, энтропия в комнате будет непрерывно возрастать, пока не зайдёт мама и не попросит вас слегка прибрать. Необходимость совершить работу означает также, что любая система будет сопротивляться уменьшению энтропии и наведению порядка. Во Вселенной та же история – энтропия как начала возрастать с Большого Взрыва, так и будет расти, пока не придёт Мама.
Мера хаоса во Вселенной

Для Вселенной не может быть применён классический вариант вычисления энтропии, потому что в ней активны гравитационные силы, а вещество само по себе не может образовать замкнутую систему. Фактически, для Вселенной – это мера хаоса.
Главнейшим и крупнейшим источником неупорядоченности, которая наблюдается в нашем мире, считаются всем известные массивные образования – чёрные дыры, массивные и сверхмассивные.
Попытки точно рассчитать значение меры хаоса пока нельзя назвать удачными, хотя они происходят постоянно. Но все оценки энтропии Вселенной имеют значительный разброс в полученных значениях – от одного до трёх порядков. Это объясняется не только недостатком знаний. Ощущается недостаточность сведений о влиянии на расчёты не только всех известных небесных объектов, но и тёмной энергии. Изучение её свойств и особенностей пока в зачатке, а влияние может быть определяющим. Мера хаоса Вселенной всё время изменяется. Учёные постоянно проводят определённые исследования, чтобы получить возможность определения общих закономерностей. Тогда будет можно делать достаточно верные прогнозы существования различных космических объектов.
Тепловая смерть Вселенной

У любой замкнутой термодинамической системы есть конечное состояние. Вселенная тоже не является исключением. Когда прекратится направленный обмен всех видов энергий, они переродятся в тепловую энергию. Система перейдёт в состояние тепловой смерти, если термодинамическая энтропия получит наивысшие значение. Вывод о таком конце нашего мира сформулировал Р. Клаузиус в 1865 году. Он взял за основу второй закон термодинамики. Согласно этому закону, система, которая не обменивается энергиями с другими системами, будет искать равновесное состояние. А оно вполне может иметь параметры, характерные для тепловой смерти Вселенной. Но Клаузиус не учитывал влияния гравитации. То есть, для Вселенной, в отличие от системы идеального газа, где частицы распределены в каком-то объёме равномерно, однородность частиц не может соответствовать самому большому значению энтропии. И всё-таки, до конца не ясно, энтропия — допустимая мера хаоса или смерть Вселенной?
Энтропия в нашей жизни

В пику второму началу термодинамики, по положениям которого всё должно развиваться от сложного к простому, развитие земной эволюции продвигается в обратном направлении. Эта нестыковка обусловлена термодинамикой процессов, которые носят необратимый характер. Потребление живым организмом, если его представить как открытую термодинамическую систему, происходит в меньших объёмах, нежели выбрасывается из неё.
Пищевые вещества обладают меньшей энтропией, нежели произведённые из них продукты выделения. То есть, организм жив, потому что может выбросить эту меру хаоса, которая в нём вырабатывается в силу протекания необратимых процессов. К примеру, путём испарения из организма выводится около 170 г воды, т.е. тело человека компенсирует понижение энтропии некоторыми химическими и физическими процессами.
Энтропия – это некая мера свободного состояния системы. Она тем полнее, чем меньшие ограничения эта система имеет, но при условии, что степеней свободы у неё много. Получается, что нулевое значение меры хаоса – это полная информация, а максимальное – абсолютное незнание.
Вся наша жизнь – сплошная энтропия, потому что мера хаоса иногда превышает меру здравого смысла. Возможно, не так далеко время, когда мы придём ко второму началу термодинамики, ведь иногда кажется, что развитие некоторых людей, да и целых государств, уже пошло вспять, то есть, от сложного к примитивному.
Выводы
Энтропия – обозначение функции состояния физической системы, увеличение которой осуществляется за счёт реверсивной (обратимой) подачи тепла в систему;
величина внутренней энергии, которая не может быть преобразована в механическую работу;
точное определение энтропии производится посредством математических расчётов, при помощи которых устанавливается для каждой системы соответствующий параметр состояния (термодинамическое свойство) связанной энергии. Наиболее отчётливо энтропия проявляется в термодинамических процессах, где различают процессы, обратимые и необратимые, причём в первом случае энтропия остаётся неизменной, а во втором постоянно растёт, и это увеличение осуществляется за счёт уменьшения механической энергии.
Следовательно, все то множество необратимых процессов, которые происходят в природе, сопровождается уменьшением механической энергии, что в конечном итоге должно привести к остановке, к «тепловой смерти». Но этого не может произойти, поскольку с точки зрения космологии невозможно до конца завершить эмпирическое познание всей «целостности Вселенной», на основе которого наше представление об энтропии могло бы найти обоснованное применение. Христианские теологи полагают, что, основываясь на энтропии, можно сделать вывод о конечности мира и использовать её для доказательства «существования Бога». В кибернетике слово «энтропия» используется в смысле, отличном от его прямого значения, который лишь формально можно вывести из классического понятия; оно означает: среднюю наполненность информацией; ненадёжность в отношении ценности «ожидания» информации.
Видео
Источники

Энтропия (от др.-греч. ἐντροπία «поворот», «превращение») – широко используемый в естественных и точных науках термин. Впервые введён в рамках термодинамики как функция состояния термодинамической системы, определяющая меру необратимого рассеивания энергии. В статистической физике энтропия характеризует вероятность осуществления какого-либо макроскопического состояния. Кроме физики, термин широко употребляется в математике: теории информации и математической статистике.
В науку это понятие вошло ещё в XIX веке. Изначально оно было применимо к теории тепловых машин, но достаточно быстро появилось и в остальных областях физики, особенно, в теории излучения. Очень скоро энтропия стала применяться в космологии, биологии, в теории информации. Различные области знаний выделяют разные виды меры хаоса:
- информационная;
- термодинамическая;
- дифференциальная;
- культурная и др.
Например, для молекулярных систем существует энтропия Больцмана, определяющая меру их хаотичности и однородности. Больцман сумел установить взаимосвязь между мерой хаоса и вероятностью состояния. Для термодинамики данное понятие считается мерой необратимого рассеяния энергии. Это функция состояния термодинамической системы. В обособленной системе энтропия растёт до максимальных значений, и они в итоге становятся состоянием равновесия. Энтропия информационная подразумевает некоторую меру неопределённости или непредсказуемости.
Энтропия может интерпретироваться как мера неопределённости (неупорядоченности) некоторой системы, например, какого-либо опыта (испытания), который может иметь разные исходы, а значит, и количество информации. Таким образом, другой интерпретацией энтропии является информационная ёмкость системы. С данной интерпретацией связан тот факт, что создатель понятия энтропии в теории информации (Клод Шеннон) сначала хотел назвать эту величину информацией.
Для обратимых (равновесных) процессов выполняется следующее математическое равенство (следствие так называемого равенства Клаузиуса), где – подведенная теплота, – температура, и – состояния, и – энтропия, соответствующая этим состояниям (здесь рассматривается процесс перехода из состояния в состояние ).
Для необратимых процессов выполняется неравенство, вытекающее из так называемого неравенства Клаузиуса, где – подведенная теплота, – температура, и – состояния, и – энтропия, соответствующая этим состояниям.
Поэтому энтропия адиабатически изолированной (нет подвода или отвода тепла) системы при необратимых процессах может только возрастать.
Используя понятие энтропии Клаузиус (1876) дал наиболее общую формулировку 2-го начала термодинамики: при реальных (необратимых) адиабатических процессах энтропия возрастает, достигая максимального значения в состоянии равновесия (2-ое начало термодинамики не является абсолютным, оно нарушается при флуктуациях).

Абсолютная энтропия (S) вещества или процесса – это изменение доступной энергии при теплопередаче при данной температуре (Btu/R, Дж/К). Математически энтропия равняется теплопередаче, деленной на абсолютную температуру, при которой происходит процесс. Следовательно, процессы передачи большого количества теплоты больше увеличивают энтропию. Также изменения энтропии увеличатся при передаче теплоты при низкой температуре. Так как абсолютная энтропия касается пригодности всей энергии вселенной, температуру обычно измеряют в абсолютных единицах (R, К).
Удельную энтропию (S) измеряют относительно единицы массы вещества. Температурные единицы, которые используются при вычислении разниц энтропии состояний, часто приводятся с температурными единицами в градусах по Фаренгейту или Цельсию. Так как различия в градусах между шкалами Фаренгейта и Ренкина или Цельсия и Кельвина равные, решение в таких уравнениях будет правильным независимо от того, выражена энтропия в абсолютных или обычных единицах. У энтропии такая же данная температура, как и данная энтальпия определенного вещества.
Подводим итог: энтропия увеличивается, следовательно, любыми своими действиями мы увеличиваем хаос.

Просто о сложном
Энтропия – мера беспорядка (и характеристика состояния). Визуально, чем более равномерно расположены вещи в некотором пространстве, тем больше энтропия. Если сахар лежит в стакане чая в виде кусочка, энтропия этого состояния мала, если растворился и распределился по всем объёму – велика. Беспорядок можно измерить, например, посчитав сколькими способами можно разложить предметы в заданном пространстве (энтропия тогда пропорциональна логарифму числа раскладок). Если все носки сложены предельно компактно одной стопкой на полке в шкафу, число вариантов раскладки мало и сводится только к числу перестановок носков в стопке. Если носки могут находиться в произвольном месте в комнате, то существует немыслимое число способов разложить их, и эти раскладки не повторяются в течение нашей жизни, как и формы снежинок. Энтропия состояния «носки разбросаны» – огромна.
Второй закон термодинамики гласит, что самопроизвольно в замкнутой системе энтропия не может убывать (обычно она возрастает). Под её влиянием рассеивается дым, растворяется сахар, рассыпаются со временем камни и носки. Эта тенденция объясняется просто: вещи движутся (перемещаются нами или силами природы) обычно под влиянием случайных импульсов, не имеющих общей цели. Если импульсы случайны, всё будет двигаться от порядка к беспорядку, потому что способов достижения беспорядка всегда больше. Представьте себе шахматную доску: король может выйти из угла тремя способами, все возможные для него пути ведут из угла, а прийти обратно в угол с каждой соседней клетки – только одним способом, причём этот ход будет только одним из 5 или из 8 возможных ходов. Если лишить его цели и позволить двигаться случайно, он в конце концов с равной вероятностью сможет оказаться в любом месте шахматной доски, энтропия станет выше.
В газе или жидкости роль такой разупорядочивающей силы играет тепловое движение, в вашей комнате – ваши сиюминутные желания пойти туда, сюда, поваляться, поработать, итд. Каковы эти желания – неважно, главное, что они не связаны с уборкой и не связаны друг с другом. Чтобы снизить энтропию, нужно подвергнуть систему внешнему воздействию и совершить над ней работу. Например, согласно второму закону, энтропия в комнате будет непрерывно возрастать, пока не зайдёт мама и не попросит вас слегка прибрать. Необходимость совершить работу означает также, что любая система будет сопротивляться уменьшению энтропии и наведению порядка. Во Вселенной та же история – энтропия как начала возрастать с Большого Взрыва, так и будет расти, пока не придёт Мама.
Мера хаоса во Вселенной

Для Вселенной не может быть применён классический вариант вычисления энтропии, потому что в ней активны гравитационные силы, а вещество само по себе не может образовать замкнутую систему. Фактически, для Вселенной – это мера хаоса.
Главнейшим и крупнейшим источником неупорядоченности, которая наблюдается в нашем мире, считаются всем известные массивные образования – чёрные дыры, массивные и сверхмассивные.
Попытки точно рассчитать значение меры хаоса пока нельзя назвать удачными, хотя они происходят постоянно. Но все оценки энтропии Вселенной имеют значительный разброс в полученных значениях – от одного до трёх порядков. Это объясняется не только недостатком знаний. Ощущается недостаточность сведений о влиянии на расчёты не только всех известных небесных объектов, но и тёмной энергии. Изучение её свойств и особенностей пока в зачатке, а влияние может быть определяющим. Мера хаоса Вселенной всё время изменяется. Учёные постоянно проводят определённые исследования, чтобы получить возможность определения общих закономерностей. Тогда будет можно делать достаточно верные прогнозы существования различных космических объектов.
Тепловая смерть Вселенной

У любой замкнутой термодинамической системы есть конечное состояние. Вселенная тоже не является исключением. Когда прекратится направленный обмен всех видов энергий, они переродятся в тепловую энергию. Система перейдёт в состояние тепловой смерти, если термодинамическая энтропия получит наивысшие значение. Вывод о таком конце нашего мира сформулировал Р. Клаузиус в 1865 году. Он взял за основу второй закон термодинамики. Согласно этому закону, система, которая не обменивается энергиями с другими системами, будет искать равновесное состояние. А оно вполне может иметь параметры, характерные для тепловой смерти Вселенной. Но Клаузиус не учитывал влияния гравитации. То есть, для Вселенной, в отличие от системы идеального газа, где частицы распределены в каком-то объёме равномерно, однородность частиц не может соответствовать самому большому значению энтропии. И всё-таки, до конца не ясно, энтропия — допустимая мера хаоса или смерть Вселенной?
Энтропия в нашей жизни

В пику второму началу термодинамики, по положениям которого всё должно развиваться от сложного к простому, развитие земной эволюции продвигается в обратном направлении. Эта нестыковка обусловлена термодинамикой процессов, которые носят необратимый характер. Потребление живым организмом, если его представить как открытую термодинамическую систему, происходит в меньших объёмах, нежели выбрасывается из неё.
Пищевые вещества обладают меньшей энтропией, нежели произведённые из них продукты выделения. То есть, организм жив, потому что может выбросить эту меру хаоса, которая в нём вырабатывается в силу протекания необратимых процессов. К примеру, путём испарения из организма выводится около 170 г воды, т.е. тело человека компенсирует понижение энтропии некоторыми химическими и физическими процессами.
Энтропия – это некая мера свободного состояния системы. Она тем полнее, чем меньшие ограничения эта система имеет, но при условии, что степеней свободы у неё много. Получается, что нулевое значение меры хаоса – это полная информация, а максимальное – абсолютное незнание.
Вся наша жизнь – сплошная энтропия, потому что мера хаоса иногда превышает меру здравого смысла. Возможно, не так далеко время, когда мы придём ко второму началу термодинамики, ведь иногда кажется, что развитие некоторых людей, да и целых государств, уже пошло вспять, то есть, от сложного к примитивному.
Выводы
Энтропия – обозначение функции состояния физической системы, увеличение которой осуществляется за счёт реверсивной (обратимой) подачи тепла в систему;
величина внутренней энергии, которая не может быть преобразована в механическую работу;
точное определение энтропии производится посредством математических расчётов, при помощи которых устанавливается для каждой системы соответствующий параметр состояния (термодинамическое свойство) связанной энергии. Наиболее отчётливо энтропия проявляется в термодинамических процессах, где различают процессы, обратимые и необратимые, причём в первом случае энтропия остаётся неизменной, а во втором постоянно растёт, и это увеличение осуществляется за счёт уменьшения механической энергии.
Следовательно, все то множество необратимых процессов, которые происходят в природе, сопровождается уменьшением механической энергии, что в конечном итоге должно привести к остановке, к «тепловой смерти». Но этого не может произойти, поскольку с точки зрения космологии невозможно до конца завершить эмпирическое познание всей «целостности Вселенной», на основе которого наше представление об энтропии могло бы найти обоснованное применение. Христианские теологи полагают, что, основываясь на энтропии, можно сделать вывод о конечности мира и использовать её для доказательства «существования Бога». В кибернетике слово «энтропия» используется в смысле, отличном от его прямого значения, который лишь формально можно вывести из классического понятия; оно означает: среднюю наполненность информацией; ненадёжность в отношении ценности «ожидания» информации.
